Desviación típica, esperanza y varianza / Distribuciones de probabilidad.

Propiedades de la desviación estándar

La desviación estándar será siempre un valor positivo o cero.

Si a todos los valores de la variable se les suma un número la desviación estándar no varía.

Si todos los valores de la variable se multiplican por un número la desviación estándar queda multiplicada por dicho número.

Si tenemos varias distribuciones con la misma media y conocemos sus respectivas desviaciones estándar se puede calcular la desviación estándar total.

Cuanta más pequeña sea la desviación estándar mayor será la concentración de datos alrededor de la media.

Por ejemplo: En una muestra de cuatro exámenes de bioestadística las calificaciones obtenidas fueron: 20, 19, 20, 19. El promedio fue 19.5 y la desviación estándar de 1.

Propiedades de la varianza

  

Cuando a todos los valores de una variable se les suma una constante, la varianza de la variable conserva el mismo valor  x+b= σ2(X+b)=  σ2

Cuando a todos los valores de una variable se les multiplica por una constante, la varianza de la variable queda multiplicada por el valor de la constante elevado al cuadrado: a*X=σ2(a*b)=a2* σ2

 3. Si X e Y son dos variables aleatorias con función de densidad o probabilidad conjunta f(x,y), la varianza de la función m(x,y) = a X ± b Y, donde a y b son constantes reales se calcula como:  σ2(ax  ±    by)=a2*  σx2 + b2* σy2 ±  2a*b*  σxy

4.  σ2 ≥0  SIEMPRE ES POSITIVA

Propiedades de la Esperanza.

Si X ¸ 0 y existe E(X), entonces E(X) ¸ 0.

Si X e Y son variables aleatorias que tienen valor esperado, entonces tambi¶en existe el
valor esperado de X + Y y se tiene
E(X + Y ) = E(X) + E(Y )

Si X e Y son variables aleatorias independientes con valor esperado, entonces existe
E(XY ) y
E(XY ) = E(X) E(Y )

Importancia de utilizar las distribuciones de probabilidad en ciencias de la salud:

Las distribuciones de probabilidad permiten describir los posibles eventos que pueden ocurrir, característica que lo convierte en un instrumento ideal para diseñar escenarios futuros y considerar las posibles tendencias así como las medidas a tomar.

Ejemplo:

El consumo diario promedio de harinas refinadas en estudiantes de medicina sigue una distribución normal de 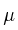 = 4 veces y 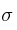= 2 veces. Determinar la probabilidad de que un estudiante de medicina consuma harinas refinadas 5 veces al día.

x= {consumo diario de harinas refinadas}

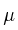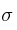z (=4 = 2)

P ( x > 5) = p ( 5-4 / 5)

P ( z > 5) = 0.2  = 1 - P ( Z < 3) = 1 - 0.5793 = 0.4207

La probabilidad de que un estudiante de medicina consuma harinas refinadas 5 veces al día es de 0.4207, determinando así a un evento relativamente probablemente. Es posible concluir dicho estudiante es propenso a padecer hiperinsulinemia.